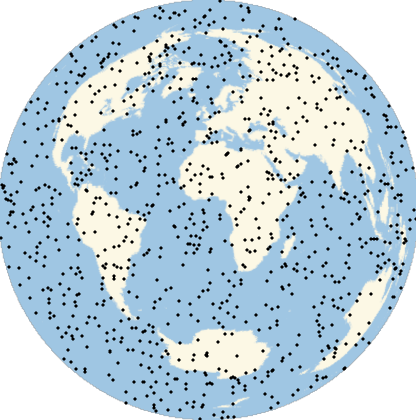
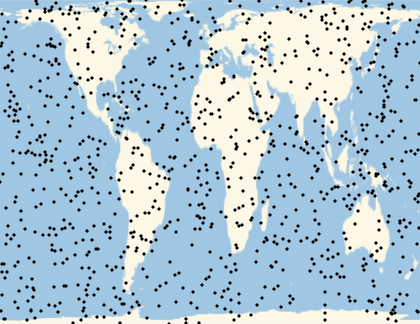
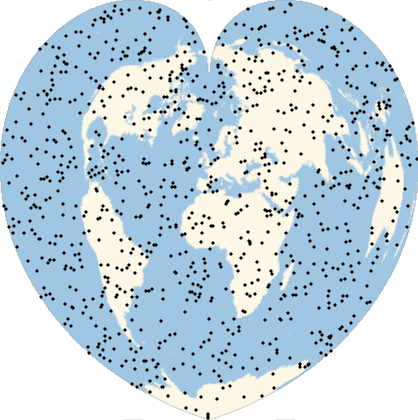
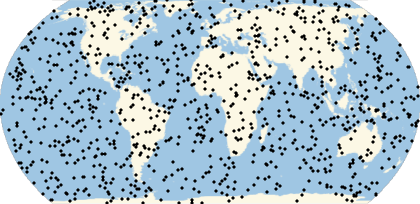
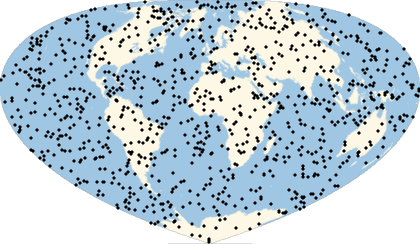
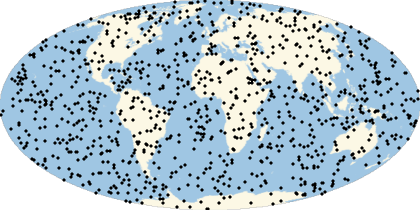
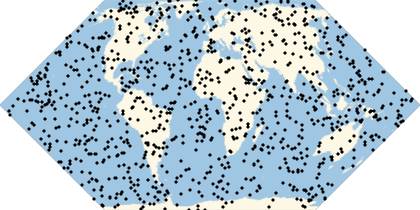
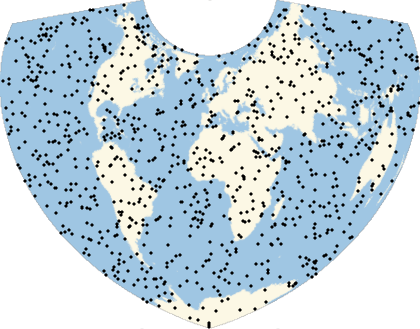
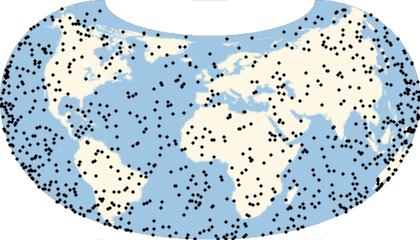
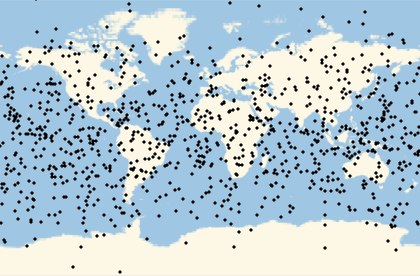
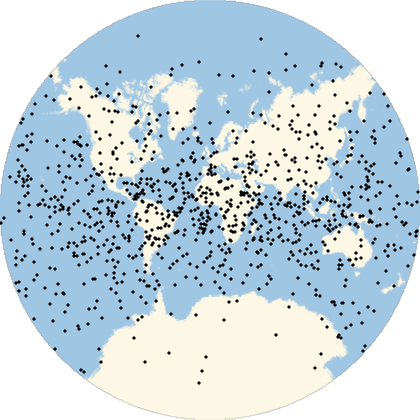
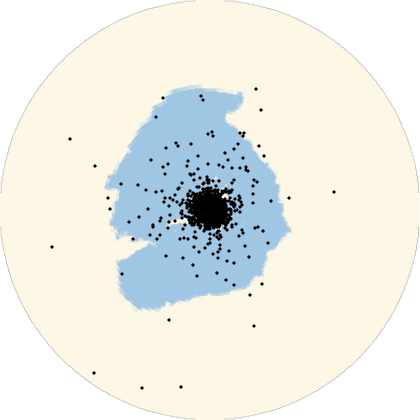
Many computations involve (or can be approximated by) the use of randomly generated locations on a given region of the Earth. A set of geo locations that is uniform in a given geo projection may not be uniform in a map with a different geo projection. This example shows the relevance of appropriately choosing the geo projection.
Generate 1000 random geo positions uniform in area:
In[3]:=
ps=RandomGeoPosition["World",1000]
Out[3]=
GeoPosition
They will look uniform in equal-area projections:
Multicolumn[Labeled[GeoGraphics[Point[ps],GeoProjection#],#]&/@{"LambertAzimuthal","Hatano","EckertII","Balthasart","Bottomley","Shield","Werner","Mollweide","TissotConicEqualArea"},3]
|
|
| ||||||
|
|
| ||||||
|
|
|
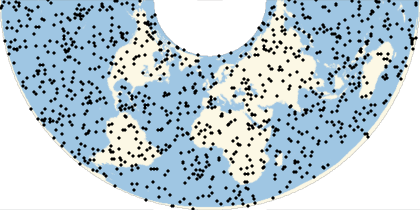
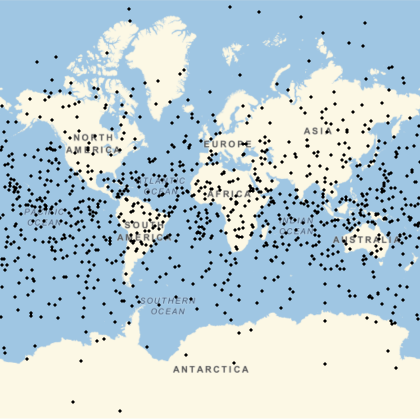
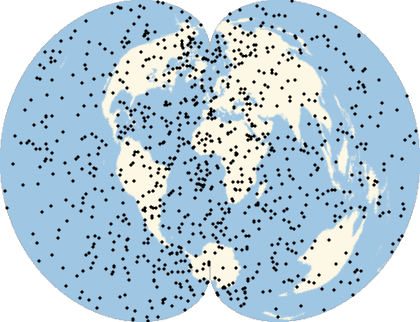
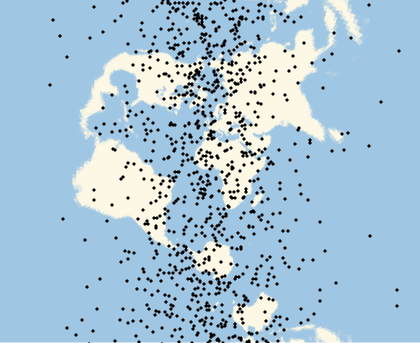
The same locations will not look uniform in non-equal-area projections:
Multicolumn[Labeled[GeoGraphics[Point[ps],GeoProjection#],#]&/@{"Mercator","Armadillo","Lagrange","AmericanPolyconic","ArdenClose","GinzburgI","TransverseMercator","LambertConicConformal","Orthographic"},3]
|
|
| ||||||
|
|
| ||||||
|
|
|